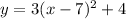The vertex form of the equation of a parabola is given to be:

where
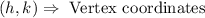
The question provides the vertex coordinates to be:
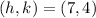
Substituting this value into the vertex form equation, we get:

We are given the coordinates of a point on the parabola to be:
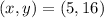
We can use this point to get the value of a in the vertex formula by substituting into the equation:
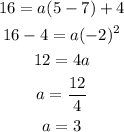
Therefore, the vertex form of the equation of the parabola is given to be: