Step-by-step explanation
Given the following points
A = (3, pi/4)
The standard from of a rectangular coordinate is given as
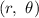
Where r = 3 and theta = pi/4
Step 1: convert radians to degrees
1 pi = 180 degrees
Therefore, pi/4 is
= 180/4
= 45 degrees
Step 2 : find cos 45 and sin 45
![\begin{gathered} \text{ Since, }\theta\text{ = 45} \\ \text{Then, cos 45 = }\frac{\sqrt[]{2}}{2}\text{ and sin 45}\frac{\sqrt[]{2}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nncd4lt3e92pgiy4b5i3pr8bu5vktmz8k4.png)
Step 3: find the x and y - coordinates
x - coordinate = r x cos 45
y - coordinate = r x sin 45
![\begin{gathered} x\text{ - coordinate } \\ \text{r = 45 and cos 45 = }\frac{\sqrt[]{2}}{2} \\ \text{x - coordinate = }\frac{3\text{ x }\sqrt[]{2}}{2} \\ x\text{- coordinate = }\frac{3\sqrt[]{2}}{2} \\ \text{y - coordinate = r x sin 45} \\ \text{y - coordinate = 3 x }\frac{\sqrt[]{2}}{2} \\ \text{y - coordiante =}\frac{3\sqrt[]{2}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j97dj4l034bex8ssc77fx3y44zjvkfqmog.png)
Therefore, the rectangular coordinate is
![(\frac{3\sqrt[]{2}}{2}\text{ , }\frac{3\sqrt[]{2}}{2})](https://img.qammunity.org/2023/formulas/mathematics/college/x2qt098kqn8ps4xfj945zc121pbw6tmlyy.png)