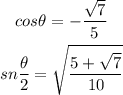Final Answer:Given: The trigonometric function
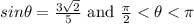
Required: To determine the exact value of
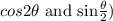
Explanation: Using the trigonometric identity.
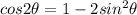
We get,
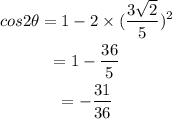
Since theta lies in the second quadrant cos will be negative.
Now,
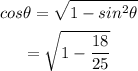
which gives
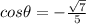
And,
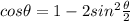
or
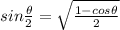
Putting the values we get
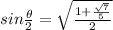
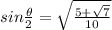
Final Answer: