Question

The headlights of an automobile are set such that the beam drops 5.00 in for each 28.0 ft in front of the car. What is the angle between the beam and the road

Answer 1

Let us make a diagram to interpret the question, we have

From the diagram above, we can see that a right-angle triangle is formed between the light beam and the road.

The opposite side of the angle theta given is 5 inches and the adjacent side is 28 feet. So we have to convert the 28 feet to inches before solving we have

`\begin{gathered} 1\text{ feet = 12 inches, so } \\ 28\text{ feet = 28}*12=336\text{ inches} \end{gathered}`

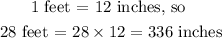
Using trigonometry SOHCAHTOA to find the angle theta, we have

`\begin{gathered} TOA\text{ tan}\theta=(opposite)/(adjacent) \\ \text{tan}\theta=\frac{5\text{ inches }}{28\text{ feet}}=\frac{5\text{ inches}}{336\text{ inches }} \\ tan\theta=(5)/(336) \\ \theta=tan^(-1)(5)/(336) \\ \theta=0.85255 \end{gathered}`

Hence the angle is 0.85 degrees to the nearest hundredth