1 Answer

Zagyi · Answer 1 · 2023-01-26T03:20:58+0000

We can draw the following picture:

then we need to find angle theta. However, in order to find theta, we must find angle x first.

Since we have a right triangle, we can apply the tangent function as:

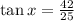
$\tan x=(42)/(25)$

then, x is given by

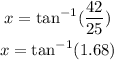
$\begin{gathered} x=\tan ^(-1)((42)/(25)) \\ x=\tan ^(-1)(1.68) \end{gathered}$

then, x is equal to

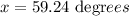
$x=59.24\text{ degr}ees$

Now, angle x and angle theta are complementary, this means that

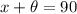
$x+\theta=90$

then, we have

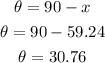
$\begin{gathered} \theta=90-x \\ \theta=90-59.24 \\ \theta=30.76 \end{gathered}$

Therefore, the angle of depression (theta) is equal to 30.76 degrees.

Please log in or register to add a comment.