Question

The bar graph shows the average number ofyears a group of people devoted to theirmost time-consuming activities. According tothe graph, a person from this group willdevote 25 years to working and eating food.The number of years working will exceed thenumber of years eating food by 19. Over allifetime, how many years will be spent oneach of these activities?years will be spent on working and years will be spent on eating food.How an Average Life Expectancy of 76 Years Is Spent3530- 25-20-15-10-I.5-Sleep Work TV Chores Food Games MallAvg Number of Years

Answer 1

Given the data below:

From the question, 25 years is devoted to eating and working. Also, the number of years working will exceed the number of years eating food by 19 year.

Let x represent the number of years devoted to eating food and y represent the number of years devoted to workings.

Thus,

`\begin{gathered} x\Rightarrow number\text{ of years for eating food} \\ y\Rightarrow number\text{ of years for working} \end{gathered}`

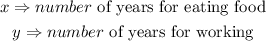
Thus, we have

`\begin{gathered} x+y=25\text{ ---equation 1} \\ y=x+19\text{ ---- equation 2} \end{gathered}`

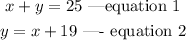
To solve the above simultaneous equations by substitution, we substitute equation 2 into equation 1.

Thus,

Substitute the value of 3 for x into equation 2.

Thus,

`\begin{gathered} y=x+19 \\ where\text{ x=3} \\ y=3+19 \\ \Rightarrow y=22 \end{gathered}`

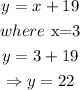
Hence,

22 years will be spent on working and 3 years will be spent on eating food.