1) Quadratic function
Step-by-step explanation:
1) We need to find the slope or the rate. If it is constant for any two points, then it will be a linear function.
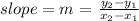
point (0, 36) and (1, 29)
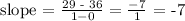
point (1, 29) and (2, 24)
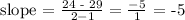
From the above we can see the slope is not constant. Hence, it is not a linear function
For a quadratic function, we check for the 2nd difference. If it is constant then it is quadratic.
First difference = change in y values (change in price)
First difference = -7, -5, -3, -1
Second difference:
-5 - (-7) = -5 + 7 = 2
-3 - (-5) = -3 + 5 = 2
-1 - (-3) = -1 + 3 = 2
The second difference for the points is the same. Hence,the function that most appropraitely represents this data is a quadratic function.