Answer:
(x-2)^2=25
Step-by-step explanation:
Given the below quadratic equation;
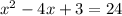
To rewrite by completing the square, the 1st step is to subtract 3 from both sides of the equation;

The 2nd step is to add half of the coefficient of x squared to both sides of the equation;

We can then factor the perfect square as;
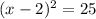
To find the solutions of the equation, we have to take the square root of both sides of the equation;
![\begin{gathered} \sqrt[]{(x-2)^2}=\sqrt[]{25} \\ x-2=(+)/(-)5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/u6mxe3gt6pet3h3r00n7ewxxazzoc53558.png)
For x 1;
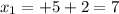
For x2;
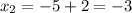
So x1 = 7 and x2 = -3.