Question

55) A typical arteriole has a diameter of 0.080 mm and carries blood at the rate of 9.6×10^−5 cm3/s. (a) What is the speed of the blood in an arteriole? (b) Suppose an arteriole branches into 8800 capillaries, each with a diameter of 6.0×10^−6 m. What is the blood speed in the capillaries? (The low speed in capillaries is beneficial; it promotes the diffusion of materials to and from the blood.)

Answer 1

a) 1.91 cm/s

b) 0.039 cm/s

Explanation:

a)

Here, since we need the velocity in cm/s, we assume that a small volume of blood passes through the section of the arteriole in a given time.

So, we have to divide the blood flow by the area of the arteriole section, therefore:

`A=\pi\cdot\mleft((d)/(2)\mright)^2`

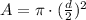
d = 0.08 mm = 0.008 cm

Replacing:

`A=3.14\cdot\mleft((0.008)/(2)\mright)^2=0.00005024=5.024\cdot10^(-5)cm^2`

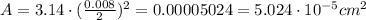
We calculate the speed by dividing the rate by the previous calculated area, like this:

`\begin{gathered} v=(q)/(A) \\ \text{Replacing} \\ v=(9.6\cdot10^(-5))/(5.024\cdot10^(-5)) \\ v=1.91\text{ cm/s} \end{gathered}`

b)

First we find the area of the section of the capillaries:

`\begin{gathered} d=6\cdot10^(-6)m=6\cdot10^(-4)cm \\ R\text{eplacing} \\ A=3.14\cdot\mleft((6\cdot10^(-4))/(2)\mright)^2 \\ A=0.0000002826=2.826\cdot10^(-7)cm^2 \end{gathered}`

Now we have to remember that the flow is dividid in equal parts, so the volume by seconds is:

`\begin{gathered} q=(9.6\cdot10^(-5))/(8800) \\ q=1.09\cdot10^(-8)(cm^3)/(s) \end{gathered}`

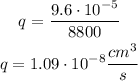
So the speed in this case is:

`\begin{gathered} v=(q)/(A) \\ v=(1.09\cdot10^(-8))/(2.826\cdot10^(-7)) \\ v=0.039\text{ cm/s} \end{gathered}`

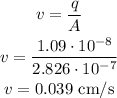
This latter speed is less than in the main arteriole.