Given:
There are given the polynomial equation:
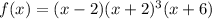
Now,
We need to find the value for the x-intercept, y-intercept, maximum, end behaviors, and multiplicity.
So,
First, find the x-intercept and y-intercept:
To find the x-intercept put 0 for y and to find the y-intercept 0 for x.
Then,
The x-intercept and y-intercept are shown below:
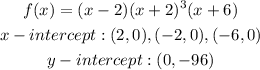
Now,
The value of maximum and minimum, end behavior and multiplicity is shown below:
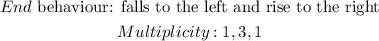
Final answer:
Hence, the value of x-intercept, y-intercept, end behaviour and multiplicity are shown below:
