When we have two equations and two variables, we have a system of equations. To solve it we first need to manipulate and combine both equations in such a way that one of them contains only one variable. This can be through many means, by multiplying one equation by a constant in such a way that when both equations are added one variable gets canceled or by isolating one variable in one equation and using that value on the other.
In this case there is no need for any manipulation, because the variable "y" is "+3y" on the first equation and "-3y" on the second one. This means that if we add both, the "y" variable will be canceled. This is done below:
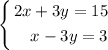
Adding both equations:
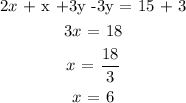
We now use the calculated value for "x" in either equation to find y. We'll use the second equation.
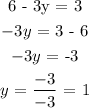
The answer to this system is x= 6 and y = 1.