ANSWER
• Amplitude: 4
,
• Period: π
,
• Phase shift: -π/8 (to the right)
Step-by-step explanation
The generic equation for a cosine function is:
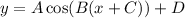
where
• A is the amplitude
,
• 2π/B is the period
,
• C is the phase shift to the left (if it's negative, then it's to the right)
,
• D is the vertical shifit
In this equation:
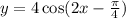
We have to rewrite it so that it looks like the equation above. We take 2 as a common factor inside the cosine expression:
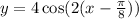
Now we clearly can see that
• A = 4
,
• C = -π/8
,
• D = 8
,
• B = 2 so the period is 2π/2 = π