Answer:
smallest angle = 84°
2nd angle = 88°
third angle = 92°
Step-by-step explanation:
Given:
The interior angles of a quadrilateral form an arithmetic sequence
The largest angle = 96°
To find:
the other angles
The sum of the interior angles of a quadrilateral = 360°
For an arithmetic sequence, there is a common difference
let the common difference = d
let the sequence:
a, a + d, a + 2d, a + 3d
a = first angle
a + 3d = last angle = 96°
if a + 3d = 96
a + 2d = 96 - common difference
a + 2d = 96 - d
a + d = 96 - 2d
a = 96 - 3d
The sequence:
96-3d, 96-2d, 96-d, 96
Sum of the angles in the interior:
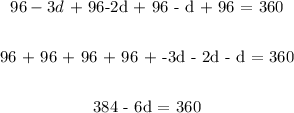
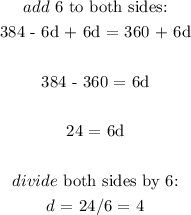
substitute for d, to get the angle measure
