Since m is a bisector of FH, we can draw the right triangle:
Now using the Pythagorean theorem, we can write:
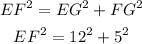
And solve:
![EF=\sqrt[]{12^2+5^2}=\sqrt[]{144+25}=\sqrt[]{169}=13](https://img.qammunity.org/2023/formulas/mathematics/college/irimnpcisnltlll02cmew2pja59aasa74m.png)
EF = 13
Since m bisects FH,
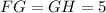
Finally, The triangle EGH is congruent with triangle EFG, by SAS. Then
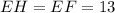
The whole answer is:
• EF = 13
,
• GH = 5
,
• EH = 13