Exponential Growth
Some real-life events grow in such a way that they can be modeled as an exponential function, given as:
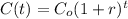
Where C(t) is the future value of the measured variable, Co is its initial value, r is the growth rate and t is the time.
We are given the following data:
Initial amount: Co=40 bacteria
Growth rate: 1 + r = 3
The bacteria triples every 4 days, thus t is the number of periods of 4 days.
Thus the model is:
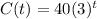
We can solve the equation
1 + r = 3
And get r = 2. Rewriting the equation:
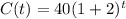
We are required to find the number of bacteria after 20 days, that is, after 20/4 = 5 periods of 4 days. Substituting:
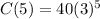
Calculating:

The colony would have 9,720 bacteria after 20 days