The ones digit of the powers of two form a pattern:
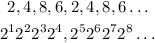
Notice that the ones digit form a repeating pattern such that even powers that are multiples of 4 have the ones digit 6.
Notice that the even powers that are not multiples of 4 have ones digit of 4
Since the given power 2054 is not a multiple of 4 but an even power it follows that the ones digit in the number 2^2054 is also 4.
The ones digit in the number 2^2054 is 4.