Question

The sum of the reciprocal of two consecutive even integers is 5/12. Find the integers.smaller integer:larger integer:

Answer 1

The smaller integer is 4 and the larger integer is 6.

Step-by-step explanation

Let the first integer be x.

Let the second integer be x + 2 (since they are consecutive even numbers)

The sum of their reciprocals is 5/12. That is

`(1)/(x)+(1)/(x+2)=(5)/(12)`

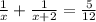
Simplify the left-hand side:

`\begin{gathered} (x+2+x)/(x(x+2))=(5)/(12) \\ \Rightarrow(2x+2)/(x^2+2x)=(5)/(12) \end{gathered}`

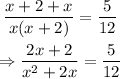
Cross-multiply:

`\begin{gathered} 12(2x+2)=5(x^2+2x) \\ 24x+24=5x^2+10x \\ \Rightarrow5x^2+10x-24x-24=0 \\ 5x^2-14x-24=0 \end{gathered}`

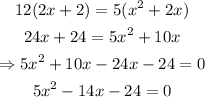
Solve the quadratic equation by quadratic formula:

`\begin{gathered} a=5,b=-14,c=-24\colon \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`
`\begin{gathered} x=\frac{14\pm\sqrt[]{(-14)^2-4(5)(-24)}}{2\cdot5} \\ x=\frac{14\pm\sqrt[]{196+480}}{10}=\frac{14\pm\sqrt[]{676}}{10} \\ x=(14\pm26)/(10) \\ \Rightarrow x=(14+26)/(10),x=(14-26)/(10) \\ x=(40)/(10),x=(-12)/(10) \\ x=4,x=-1.2 \end{gathered}`

Since the number is an even integer, therefore, we have that:

`x=4`

That is the smaller integer.

Therefore, the larger integer is:

`\begin{gathered} x+2 \\ \Rightarrow4+2 \\ \Rightarrow6 \end{gathered}`

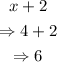
Hence, the smaller integer is 4 and the larger integer is 6.