As per given by the question,
There are given that a sides and length of the four triangle.
Now,
Check one-by-one, whether triangles are right triangle or not.
Then,
For check the triangle is right triangle or not, use pythagoras theorem.
Now,
For first triangle,
The side is given,
Suppose ,
![A=12,\text{ B=24, and C=}\sqrt[]{439}](https://img.qammunity.org/2023/formulas/mathematics/college/hm9eocgmc18hceebof0twtwx7sa1z8634a.png)
Then,
From the pythagoras theorem,
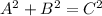
Put the value of A, B, and C in above formula;
So,
![\begin{gathered} 12^2+24^2=(\sqrt[]{439})^2 \\ 144+576=439 \\ 720\\e439 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q55cakx21w8bbv61tt1clej30cp5knu0kh.png)
Hence, first triangle is not a right angle triangle.
Now,
For second triangle,
![A=14,\text{ B=18, and C=}\sqrt[\square]{520}](https://img.qammunity.org/2023/formulas/mathematics/college/eb2ukr9wuhjab2c8495dx1yvcoqfxxg2v8.png)
Then,
![\begin{gathered} A^2+B^2=C^2 \\ 14^2+18^2=(\sqrt[]{520})^2 \\ 196+324=520 \\ 520=520 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1gqy11pp7lgv7rzphcw9c2lhgwnhljmnmq.png)
Hence, the second triangle is right angle triangle.
Now,
For third triangle,
![\begin{gathered} A^2+B^2=C^2 \\ 16^2+18^2=(\sqrt[]{421})^2 \\ 256+324=421 \\ 580\\e421 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d49h0zlpn4pk0m3cpra62h2ebz7s86tshe.png)
Hence, the third triangle is not a right angle triangle.
Now,
For fourth triangle,
![\begin{gathered} A^2+B^2=C^2 \\ 15^2+18^2=(\sqrt[]{549})^2 \\ 225+324=549 \\ 549=549 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a3srixqjeoxq56qg7z962npjdrk7gncs27.png)
Hence, the fourth triangle is also a right triangle.
So,
The second and fourth triangle is right angle triangle.