We are given the following function
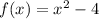
Let us perform the transformations on the above function.
Part A: Write a function that shifts f(x) left 5 units
The following rule is used to shift f(x) left by b units

Let us apply the above rule

Part B: Write a function that shifts f(x) right 8 units
The following rule is used to shift f(x) right by b units
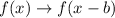
Let us apply the above rule
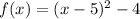
Part C: Write a function that horizontally stretches f(x) by 1 unit
The following rule is used to horizontally stretch the f(x) by b units
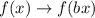
Let us apply the above rule
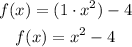
Part D: Write a function that horizontally compresses f(x) by 6 units.
The following rule is used to horizontally compress the f(x) by b units.
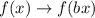
Let us apply the above rule
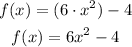
Part E: Write a function that reflects f(x) about the x-axis.
The following rule is used to reflect f(x) about the x-axis
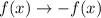
Let us apply the above rule
