Question

Which statements about the line that passes through (−2, 0) and (2, −4) are true? Select all that apply.A.The slope of the line is 1.B.The line intersects the y-axis at (0, −2).C.The equation of the line is y = −x − 2.D.The line intersects the x-axis at (−2, 0).

Answer 1

Given that the line passes through the points (-2,0) and (2, -4)

Slope of the line:

The slope m of the line is calculated as

`\begin{gathered} m\text{ = }\frac{\text{rise}}{run}=(y_2-y_1)/(x_2-x_1) \\ \text{where } \\ y_1=0 \\ x_1=-2 \\ y_2=-4 \\ x_2=2 \end{gathered}`

Thus,

`m=(-4-0)/(2-(-2))=-(4)/(4)=-1`

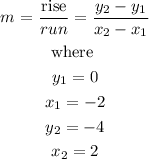
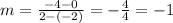
Thus, the slope of the line is -1

The equation of the line:

The equation of a line passing through two points is given as

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where m=}(y_2-y_1)/(x_2-x_1) \end{gathered}`

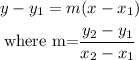
Thus, we have

`\begin{gathered} y-0=-1(x-(-2)) \\ y=-1(x+2) \\ y=-x-2 \end{gathered}`

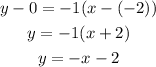
Thus, the equation of the line is y= -x-2

The line intersects the y-axis at (0,2):

The point at which the line intersects the y-axis is the intercept. At the intercept, the value of x equals zero.

Thus, the corresponding value of y when x equals zero will be

`y=-x-2=-0-2=-2`

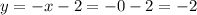
Thus, the line intersects the y-axis at (0,2)

The line intersects the x-axis at (-2,0):

When the line intersects the x-axis, the value of y equals zero. Thus, the corresponding value of x when y equals zero will be

`\begin{gathered} y=-x-2 \\ 0=-x-2 \\ \text{collecting like terms, we have} \\ 0+2=-x \\ x=-2 \end{gathered}`

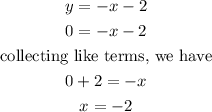
Thus, the line intersects the x-axis at (-2,0)

Hence, options A, B, C, and D are true.