We are given that a block is pushed upwards vertically by a force that has an angle of 25 degrees. To determine the work done by the force "F" we will first add the forces in the vertical direction:
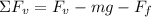
Where:

Now, we determine the vertical component of the force. To do that we will use the trigonometric function sine since it is defined as:
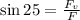
Now we multiply both sides by the force "F":
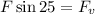
Now we replace this in the sum of vertical forces:
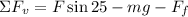
To determine the friction force we will use the following relationship:
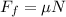
Where:
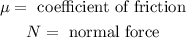
The coefficient of friction is given therefore, we need to determine the magnitude of the normal force. To do that we will add the forces in the horizontal direction:
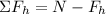
We determine the horizontal component of the force using the trigonometric function cosine:
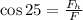
Now we multiply both sides by "F":
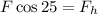
Now we substitute in the sum of forces:
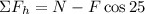
Since there is no movement in the horizontal direction the sum of the forces must be equal to zero:
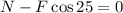
Now we solve for N by adding "Fcos25" to both sides:
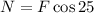
Now we substitute this value in the relationship for friction:
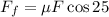
Now we substitute the friction force in the vertical sum of forces:

Since the velocity is constant this means that the acceleration is zero and therefore, the sum of the forces is zero:

Now we solve for "F". To do that we will add "mg" to both sides:
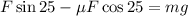
Now we take "F" as a common factor:
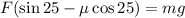
Now we divide by the factor of "F":
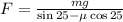
Now we substitute the given values:
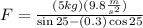
Solving the operations:
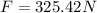
Now, to determine the work done by the force we use the following formula:
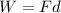
Where:
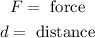
Substituting the values we get:
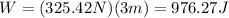
Therefore, the work done by the force is 976.27 Joules.
Now we determine the work done by gravity. This is equivalent to the work done by the weight therefore, it is:
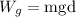
Where "m" is mass, and "g" is the acceleration of gravity. Their product is the weight.
Substituting the values:
![W_g=(5\operatorname{kg})(9.81(m)/(s^2))(3m)]()
Solving we get:
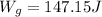
The magnitude of the work done by gravity is 147.15 Joules.
Finally, to determine the normal force we use the equation we got from the sum of forces in the horizontal direction:
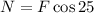
Now we substitute the value we found for "F":
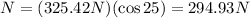
Therefore, the normal force is 294.93 Newtons.