Question

The sum of two numbers is 2490 . Find the numbers, if 8.5% of the first one is equal to 6.5% of the other .

Answer 1

You give to each number a letter:

Number 1: x

Number 2: y

The sum of two numbers is 2490:

`x+y=2490`

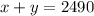
8.5% of x is equal to 6.5% of y:

`x\cdot(8.5)/(100)=y\cdot(6.5)/(100)`

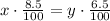
You use the equations above to find the numbers by substitution method:

1. Solve one of the variables in the first equation:

`x=2490-y`

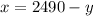
2. Substitute the variable x in the second equation by the value in step 1:

`(2490-y)\cdot(8.5)/(100)=y\cdot(6.5)/(100)`

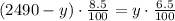
3. Solve the equation in step 2 and find the value of y:

`(2490-y)0.085=0.065y`

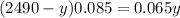
Remove parenthesis multipliying 0.085 for both terms in the parenthesis:

`211.65-0.085y=0.065y`

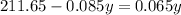
Add 0.085y in both sides of the equation:

`\begin{gathered} 211.65-0.085y+0.085y=0.065y+0.085y \\ 211.65=0.15y \end{gathered}`

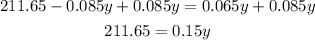
Divide into 0.15 both sides of the equation:

`\begin{gathered} (211.65)/(0.15)=(0.15)/(0.15)y \\ \\ 1411=y \end{gathered}`

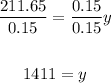
4. Use the value of y to find x:

`\begin{gathered} x=2490-y \\ x=2490-1411 \\ x=1079 \end{gathered}`

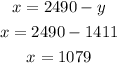
Then, the numbers are x=1079 and y=1411