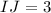Hi, can you help me to solve this exercise, please!!

Question

asked Apr 16, 2023 215k views

1 Answer

RHicke · Answer 1 · 2023-04-23T02:40:37+0000

Question:

Solution:

Step 1: Find the missing interior angle x:

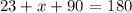
$23+x+90\text{ = 180}$

this is equivalent to:

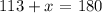
$113+x\text{ = 180}$

solving for x, we obtain:

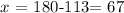
$x\text{ = 180-113= 67}$

Thus, we obtain the following right-triangle:

Step 2: Apply the proper trigonometric identity:

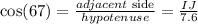
$\cos (67)=\frac{adjacent\text{ side}}{hypotenuse}=(IJ)/(7.6)$

that is:

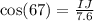
$\cos (67)=(IJ)/(7.6)$

solving for IJ, we obtain:

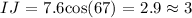
$IJ\text{ = 7.6cos(67) = 2.9}\approx3$

so that, we can conclude that the correct answer (approximate to the nearest tenth) is:

$IJ\text{ = 3}$