6. A is 60 miles from B. An automobile at A starts for B at the rate of 20 miles an hour at
the same time that an automobile at B starts for A at the rate of 25 miles an hour. How
long will it be before the automobiles meet?
Rate
Time
Distance
Ryan
Castel
Step 1
Assume they are were they meet
Let
Ryan goes from A to B
rate = 20 miles per hour
time = unknow (t), this time is the same for the two automobile
distance1=unknown( x)
Castel goes from B to A
rate2= 25 miles per hour
time= unknown(t)
distance2 =unknown(y)
we also know that distance from A to b is 60 miles, so
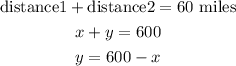
Step 2
make the equations
for Ryan
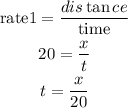
For Castel
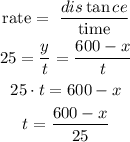
Now, the time is the same
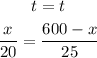
solve for x
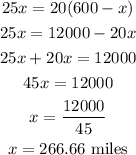
now, with the value of x, replace it to find t
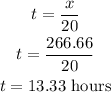
finally, replace the value of x to find y