The formula used to calculate the nth term of a geometric sequence is given to be:
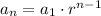
From the question, we are given the following parameters:
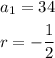
Therefore, we can calculate the first 5 terms as follows:
First Term: 34
Second Term: -17
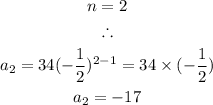
Third Term: 8.5
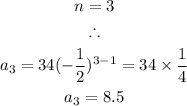
Fourth Term: -4.25
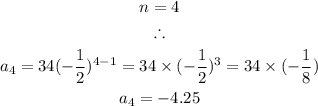
Fifth Term:
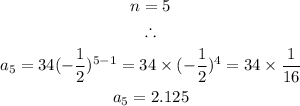
The first five terms are 34, -17, 8.5, -4.25, and 2.125.