1 Answer

Basketballnewbie · Answer 1 · 2023-01-20T04:34:32+0000

Given,

The mean of the test score is 1013.

The standard deviation of the test score is 125.

The percentage of cutoff is 9%.

The z score at 9% is,

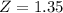
The z score is calculated as,

$z=\frac{X-\operatorname{mean}}{s\tan dard\text{ deviation}}$

Substituting the value of z, mean and standard deviation then,

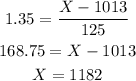
$\begin{gathered} 1.35=(X-1013)/(125) \\ 168.75=X-1013 \\ X=1182 \end{gathered}$

Hence, the cutoff for the top 9% is 1182.

Please log in or register to add a comment.