ANSWER:
A. The distance between the plane and the airport is 94875 feet.
B. The distance between a point on the ground directly below the plane and the airport is 88573 feet.
Explanation:
The first thing to do is find the interior angle of the right triangle formed by the airport plane and a point directly below the plane. Just like this:
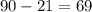
The distance from the airplane to the airport is the hypotenuse (we don't know it), and the height of the airplane is given as 34000 feet.
By means of the trigonometric cosine function we can calculate the hypotenuse, that is, the distance from the plane to the airport, like this:
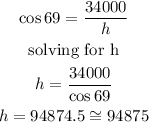
Therefore, the distance between the plane and the airport is 94875 feet.
The distance between a point on the ground directly below the plane and the airport is the opposite side 69 degrees, therefore we can use the trigonometric function sine to calculate this distance since the value of the hypotenuse is already known:
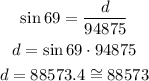
Therefore, the distance between a point on the ground directly below the plane and the airport is 88573 feet.