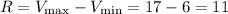Question

ws the lengths of the 12 trailers sold at a store last month. Trailers Sold + 6 7 8 9 10 11 12 13 14 15 16 17 Length (feet) hent about the data is true? R is 7. and the range is 17. QR is 7, and the range is 11. QR is 2.75. and the range is 17. QR is 2.75, and the range is 11.

Answer 1

The IQR is 7, and the range is 11

Explanation:

The first thing is to identify the extremes of the picture, which is the minimum value and the maximum value

`\begin{gathered} V_(\min )=6 \\ V_(\max )=17 \end{gathered}`

We calculate the median of the data, which is the number of the half:

`m=(11+12)/(2)=11.5`

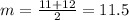
We calculate the median of Q1 (6 - 11.5) and the median of Q3 (11.5 - 17)

`\begin{gathered} m_(Q1)=8 \\ m_(Q2)=15 \end{gathered}`

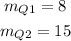
The IQR is the difference between Q3 and Q1 medians, therefore

`\begin{gathered} \text{IQR}=m_(Q3)-m_(Q1)=15-8 \\ \text{IQR = 7} \end{gathered}`

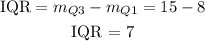
The range is the difference between the minimum and maximum value, therefore

`R=V_(\max )-V_(\min )=17-6=11`