Question

a Customers of a phone company can choose between two service plans for long distance calls. The first plan has a $15 monthly fee and charges an additional 0.11 for each minute of callsThe second plan has an $8 monthly fee and charges an additional for each minute of calls For how many minutes of calls will the costs of the two plans be equal?

Answer 1

Assume that the number of the minutes of calls is x minutes

For the first plan:

There is a monthly amount of $15

Additional cost $0.11 for each minute

Then the cost of the calls is

`15+0.11x`

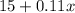
For the second plan:

There is a monthly amount of $8

Additional cost $0.16 for each minute

Then the cost of the calls is

`8+0.16x`

If the two plans cost the same, then equate the two expressions above

`8+0.16x=15+0.11x`

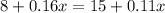
Now let us solve the equation to find x

Subtract 8 from both sides

`\begin{gathered} 8-8+0.16x=15-8+0.11x \\ 0.16x=7+0.11x \end{gathered}`

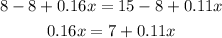
Subtract 0.11x from both sides

`\begin{gathered} 0.16x-0.11x=7+0.11x-0.11x \\ 0.05x=7 \end{gathered}`

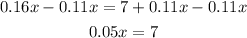
Divide both sides by 0.05

`\begin{gathered} (0.05x)/(0.05)=(7)/(0.05) \\ x=140 \end{gathered}`

For 140 minutes the two plans have equal cost