Bob has 120 trees in the grove. Each tree produces about 650 oranges.
Bob wants to maximize this orange production by adding new trees to the grove. Space limitations and sunlight make it to reduce each tree's production by 5 oranges per tree added.
The total number of oranges actually produced is the product of the number of trees by the number of oranges per tree, that is, 120 * 650 = 78,000 oranges.
Now suppose Bob adds x trees to the grove. The new number of trees is 120 + x and each tree now produces 650 - 5x oranges.
The number of oranges produced under this new condition is:
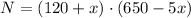
Operating:
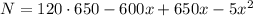
Simplifying:
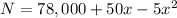
To maximize the number of oranges, we use derivatives:
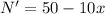
Equating the first derivative to 0:
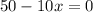
Solving for x:
x = 50 / 10 = 5
This means that Bob should add only 5 more orange trees to maximize production.
The new number of trees would be 120+5= 125 trees
Each tree would produce 650 - 5*5 = 625 oranges
The total production would be 125*625 = 78,125 oranges