First, let's draw a scheme representing the measures in the text. Let's call the shorter building as A and the taller building as B.
Using this scheme, we can see that we have 2 right triangles. The height of the taller building(let's call it hB), is given by the following relation

Then, calculating the height we have
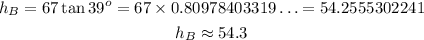
The difference between the height of the smaller building(let's call it hA) and the taller building, is given by

Solving for h_A, we have
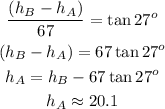
The height of the smaller building is 20.1m and the height of the taller building is 54.3m.