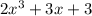Question

Use the given length and area of a rectangle to express the width algebraically. (Simplify your answer completely.)Length is 3x − 4Area is 6x^4 − 8x^3 + 9x^2 − 3x − 12

Answer 1

Given the expression that represents the length of the rectangle:

`3x-4`

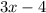
And the expression that represents the area of the rectangle:

`6x^4-8x^3+9x^2-3x-12`

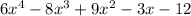
You need to remember that the formula for calculating the area of a rectangle is:

`A=lw`

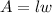
Where "l" is the length and "w" is the width.

If you solve for the width, you get this formula:

`w=(A)/(l)`

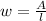
Therefore, you can write this expression to represent the width of the given rectangle:

`(6x^4-8x^3+9x^2-3x-12)/(3x-4)`

In order to simplify it, you can follow these steps:

1. Rewrite this term in this form in the numerator:

`3x=-12x+9x`

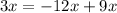
Then:

`=(6x^4-8x^3+9x^2-12x+9x-12)/(3x-4)`

2. Group pair of terms in the numerator and factor the Greatest Common Factor (the largest factor each group has in common) out of the parentheses:

`=((6x^4-8x^3)+(9x^2-12x)+(9x-12))/(3x-4)`
`=(2x^3(3x-4)+3x(3x-4)+3(3x-4))/(3x-4)`

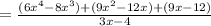
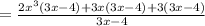
3. Factor this Greatest Common Factor out in the numerator:

`3x-4`

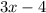
You get:

`=((3x-4)(2x^3+3x+3))/(3x-4)`

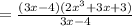
4. By definition:

`(a)/(a)=1`

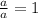
Therefore, you get:

`=2x^3+3x+3`

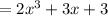
Hence, the answer is:

`2x^3+3x+3`