Arc Length
The length of an arc formed in a circle is given by:
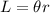
Where r is the radius of the circle and θ is the angle.
We are given the distance VZ = 15 cm. Since VZ is a radius of the circle, then r = 15 cm.
Part I. Find the length of VW.
Before calculating the required length, we need to find the angle of the arc VW. We proceed as follows.
VY is the diameter of the circle, thus angle VY is 180°. Note angle VX is marked as a right angle, that is, measures 90°.
This means that the sum of arcs XY and VW must be 90°:
arc XY + arc VW = 90°
Since we know that arc XY = 26°, then:
arc VW = 90° - 26° = 64°
Now we know the value of the angle, we can calculate the required arc length.
Recall that we need to express the angle in radians, thus we multiply by pi by 180:
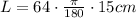
Calculating and rounding to the nearest tenth:
L = 16.8 cm
Part II. Find the length of arc UXV.
This arc starts in U, goes all the way round through X, and finishes in V.
Please note the required length can be calculated with angle UV because
UV + UXV = 360°
Angle UV is a vertical angle with YX. Vertical angles are congruent, thus UV = 26°
We find that UXV = 360° - 26° = 334°
Calculate the arc length:
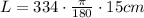
Calculating and rounding to the nearest tenth:
L = 87.4 cm