Question

f(x) = (2x + 4)/(3x + 2) Consider the function For this function there are two important intervals: (- ∞, A) and (A, ∞) where the function is not defined at A. Find A

Answer 1

Given:

The function

`f(x)=(2x+4)/(3x+2)`

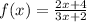
Required:

Find all parts.

Step-by-step explanation:

Domain:

The domain of a function is the set of all possible inputs for the function.

Increasing and Decreasing of a function:

The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain. If f′(x) > 0 at each point in an interval I, then the function is said to be increasing on I. f′(x) < 0 at each point in an interval I, then the function is said to be decreasing on I.

Concavity:

A function f is concave up (or upwards) where the derivative f' is increasing. This is equivalent to the derivative of f', which is f'', being positive. Similarly, f is concave down (or downwards) where the derivative f' is decreasing (or equivalently, f'', is negative).

The graph of a function:

Now, the function defined on

`=(-\infty,-(2)/(3))\cup(-(2)/(3),\infty)`

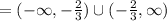
Where the function is not defined at A

`A\text{ }is\text{ }x=-(2)/(3)`
`\begin{gathered} \text{ For each of the following interval function is decreasing on}: \\ (-\infty,-(2)/(3))\cup(-(2)/(3),\infty). \end{gathered}`

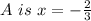
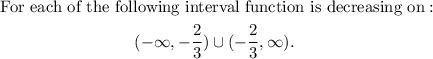
Also,

`\begin{gathered} \text{ Function is concave upward on }(-(2)/(3),\infty). \\ \text{ Function is concave downward on }(-\infty,-(2)/(3)). \end{gathered}`

Answer:

Completed the question.