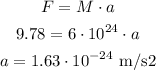5)
a)
In order to calculate the force acting on the masses, we can use the formula below:
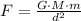
Where G is the gravitational constant (G = 6.674 * 10^-11), M is the greater mass, m is the smaller mass and d is the distance between the masses.
So, for M = 6 * 10^24 kg, m = 1 kg and d = 6.4 * 10^6 m, we have:
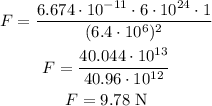
b)
The force calculated in item a) will act on both masses, therefore the force acting on the larger object is also F = 9.78 N.
c)
The acceleration can be calculated using the second law of Newton:
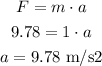
d)
Using the second law of Newton again, we have: