Question

#14A rocket is launched from the ground with an initial upward velocity of 56feet per second, After how many seconds will it return to the ground?a) write a quadratic equation that models the situation, andb) solve the equation to answer the question.

Answer 1

14)

Answer:

Step-by-step explanation:

We would apply newton's formula of motion which is expressed as

h = ut + 1/2gt^2

where

h is the height

u is the initial velocity

g is the acceleration due to gravity in feet per second^2 = -32ft/s^2

From the information given,

h = 56t - 1/2 x 32 x t^2

h = 56t - 16t^2

The quadratic equation is expressed as

h = - 16t^2 + 56t

where

h represents the height of the rocket in feet

t represents the time in seconds

By the time the rocket returns to the ground, h = 0. We would substitute h = 0 into the equation and solve for t. We have

0 = - 16t^2 + 56t

The standard form of a quadratic equation is expressed as

y = ax^2 + bx + c

By comparing both equations,

a = - 16

b = 56

c = 0

The general formula for solving quadratic equations is expressed as

`\begin{gathered} x\text{ = }\frac{-\text{ b}\pm√(b^2-4ac)}{2a} \\ x\text{ = }\frac{-\text{ 56 }\pm\sqrt{56^2-4(-\text{ 16 }*0)}}{2\text{ }*-\text{ 16}} \\ \frac{-\text{ 56 }\pm56}{-\text{ 32}} \\ x\text{ = }\frac{-\text{ 56 - 56 }}{-32}\text{ or x = }\frac{-\text{ 56 + 56}}{-\text{ 32}} \\ x\text{ = 3.5 or x = 0} \end{gathered}`

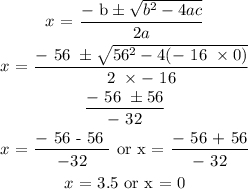
Replacing x with t, we have

t = 3.5

It will return to the ground after 3.5 seconds