Given the function
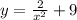
since y=(f(g(x))
We need to find f(x) and g(x)
f(x) is
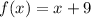
then
g(x)
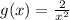
then
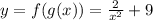
We have
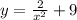
replace then
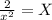
now we have
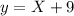
now we are give that
y=(f(g(x))
this means that for a function f(x) the value of x is replace with the function g(x)
then the only option to complete this statement is that
f(x)=X+9
but remember X=