Given:
• Length of base(cube) = 6 ft
,
• Height of square prism = 20 ft
,
• Height of pyramid =4 ft
Since it is a composite figure, the surface of some sides will not be included in the surface area.
Let's solve for the following:
• (a). The surface area of the pyramid.
To find the surface area of the pyramid, apply the formula:
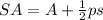
Where:
A is the area of the base
p is the perimeter of the base
s is the slant height.
To find the slant height, apply Pythagorean theorem:
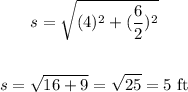
We have:
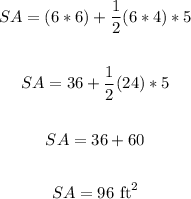
The surface area of the pyramid is 96 ft².
• (b). Surface area of the square prism.
Apply the formula:
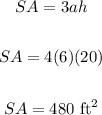
The surface area of the square prism is 480 ft².
• (c). Surface area of the cube.
To find the surface area of the cube, we have:
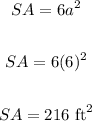
The surface area of the cube is 216 ft²
The total surface area will be:
T = Surface area of pyramid + surface area of prism + surface area of cube - area of base
T = 96 + 480 + 216 - 36
T = 756 ft²
ANSWER:
Surface area of the pyramid is 96 ft².
Surface area of the square prism is 480 ft².
Surface area of the cube is 216 ft²
Total surface area is 756 ft²