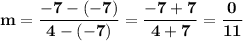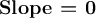Question

Find the slope of the line passing through the points (-7, 4) and (-7, -3). slope: Find the slope of the line passing through the points (-7.-7) and (4.-7). slope:

Answer 1

1. Not defined
2. Zero

In-depth explanation:

Hi! The question is asking us to find the slope of the line, given that it passes through the points (-7,4) and (-7,3).

To find the slope, I use the Slope Formula:

`\Large\boxed{\boxed{\mathbf{m=(y_2-y_1)/(x_2-x_1)}}}`

Where:

• m = slope
• y₂ = the y-coordinate of the second point
• x₂ = the x-coordinate of the second point
• y₁ = the y-coordinate of the first point
• x₁ = the x-coordinate of the first point

Plug in the data:

`\bf{m=(-3-4)/(-7-(-7))=(-7)/(-7+7)}=(-7)/(0)}`

`\bf{m=not\:de fined}`

`\rule{350}{1}`

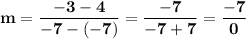
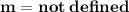
Now let's find the slope between the second pair of points.

The points are: (-7,-7) and (4,-7), so let's go ahead and plug them in:

`\bf{m=(-7-(-7))/(4-(-7))=(-7+7)/(4+7)}=(0)/(11)}`

`\large\textbf{Slope = 0}`

Answer 2

Given the points ( -7 , 4 ) and (-7 , -3 )

The slope of the line passing through the given points is calculated as following :

`slope=(rise)/(run)=(y_2-y_1)/(x_2-x_1)=(-3-4)/(-7-(-7))=(-7)/(-7+7)=-(7)/(0)=0`

So, the slope of the line = 0

which mean the line will be parallel to the x- axis