Question

Which function is an even function?

OA. y=2sin?(4.c)+5sins
O B. y=tan?()–2tant
OC y = 3c032(3.r)-COSI
OD. y=csc2(5—27) -
-CSCI

Answer 1

An even function is defined as:

`f(-x)=f(x)`

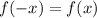
That is, the function evaluated at the negative of its argument must be the same function. Here is a list of even trigonometric functions:

`\begin{gathered} \cos (-x)=\cos (x) \\ \csc (-x)=\csc (x) \end{gathered}`

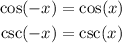
The rest of the trigonometric functions are not even. Now, from A we see that the function has a sin(x) term, which is not even (the term sin²(4x) is even because any function to the square are even functions). We conclude that function A is not even.

From B, we see that there is a tan(x) term, which is not even. We conclude that function B is not even.

From C, both terms have a cosine, which is even, so function C is an even function.

From D, the cosine square term has a complex argument, so we need to explore it in depth.