Question

The following are all 5 quiz scores of a student in a statistics course. Each quite was graded on a 10-point scale. Assuming that these scores constitute an entire population, find the standard deviation of the population. ROUND YOUR ANSWER TO TWO DECIMAL PLACES

Answer 1

The following are all 5 quiz scores of a student in a statistics course. Each quite was graded on a 10-point scale

Where, n = 5

`9,10,9,8,9`

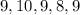
To find the standard deviation, firstly we will find the mean

`Mean=(9+10+9+8+9)/(5)=(45)/(5)=9`

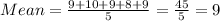
Secondly, we will subtract the mean from each score

The standard deviation will be

`\sigma=\sqrt{(\sum^(x-mean)^2)/(n)}=\sqrt{(2)/(5)}=√(0.4)=0.63\text{ \lparen two decimal places\rparen}`

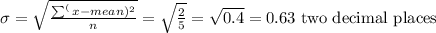
Hence, the standard deviation is 0.63 (two decimal places)