Answer
1) Rate of change of water in the tank = -⅓ gallons per minute = -0.333 gallons per minute.
2) It would take the tank an extra 9 minutes to drain completely from the current level of 3 gallons of water.
3) THe tank must have been draining for 15 minutes before Jada first arrives at the water tank.
Step-by-step explanation
1) The rate of leakage or rate of change of the volume of water in the tank is given as
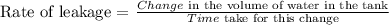
For this tank, Jada first sees the water in the tank at 5 gallons and then, she then sees the water in the tank at 3 gallons, 6 minutes later.
Change in the volume of water in the tank = (Final volume) - (Initial volume)
Change in the volume of water in the tank = 3 - 5 = -2 gallons
Time taken for this change = 6 minutes
Rate of change of water in the tank = (-2/6) = -⅓ gallons per minute = -0.333 gallons per minute.
2) How many minutes will it take for the tank to be completely empty?
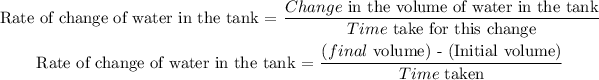
If we want to find the time it would take for the tank to now be empty, from the current volume of 3 gallons that it is now,
Final volume = 0 gallon
Initial volume = 3 gallons
Time taken = t = ?
Rate of change of water in the tank = -0.333 gallons per minute.

3) Before Jada's arrival, the tank must have been full at 10 gallons.
When she first arrives, she meets the tank at 5 gallons.
The time it takes the tank to drain from 10 gallons to 5 gallons is what we need to find now
Final volume = 5 gallon
Initial volume = 10 gallons
Time taken = t = ?
Rate of change of water in the tank = -0.333 gallons per minute.

Hope this Helps!!!