Given the function:
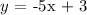
The rate of change (slope) is expressed as

The slope is also evaluated from the general equation of the line function expressed as
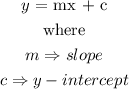
In the given function,
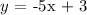
This implies that in comparison with the general equation of the line function, the rate of change (slope) is evaluated to be -5.
In option A,
taking any two points for (x₁, y₁) and (x₂, y₂),
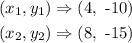
the slope is evaluated to be
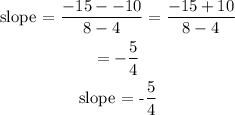
In option B,
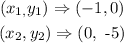
the slope is evaluated to be
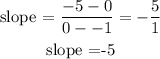
In option C,
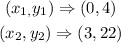
the slope is evaluated to be

In option D,
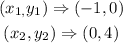
the slope is thus evaluated as
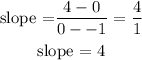
Since the slope in option B is evaluated to be -5 which is equivalent to the slope of the function in question, the correct option is B.