1 Answer

Waleed Qidan · Answer 1 · 2023-09-15T14:31:59+0000

Given the function:

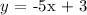
$y\text{ = -5x + 3}$

The rate of change (slope) is expressed as

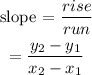
$\begin{gathered} \text{slope = }(rise)/(run) \\ =(y_2-y_1)/(x_2-x_1) \end{gathered}$

The slope is also evaluated from the general equation of the line function expressed as

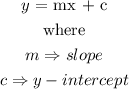
$\begin{gathered} y\text{ = mx + c} \\ \text{where} \\ m\Rightarrow slope \\ c\Rightarrow y-intercept \end{gathered}$

In the given function,

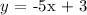
$y\text{ = -5x + 3}$

This implies that in comparison with the general equation of the line function, the rate of change (slope) is evaluated to be -5.

In option A,

taking any two points for (x₁, y₁) and (x₂, y₂),

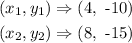
$\begin{gathered} (x_1,y_1)\Rightarrow(4,\text{ -10)} \\ (x_2,y_2)\Rightarrow(8,\text{ -15)} \\ \end{gathered}$

the slope is evaluated to be

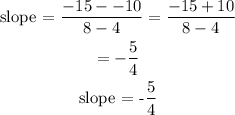
$\begin{gathered} \text{slope = }(-15--10)/(8-4)=(-15+10)/(8-4) \\ =-(5)/(4) \\ \text{slope = -}(5)/(4) \end{gathered}$

In option B,

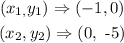
$\begin{gathered} (x_(1,)y_1)\Rightarrow(-1,0) \\ (x_2,y_2)\Rightarrow(0,\text{ -5)} \end{gathered}$

the slope is evaluated to be

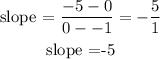
$\begin{gathered} \text{slope = }(-5-0)/(0--1)=-(5)/(1) \\ \text{slope =-5} \end{gathered}$

In option C,

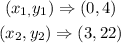
$\begin{gathered} (x_(1,)y_1)\Rightarrow(0,4) \\ (x_2,y_2)\Rightarrow(3,22\text{)} \end{gathered}$

the slope is evaluated to be

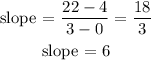
$\begin{gathered} \text{slope = }(22-4)/(3-0)=(18)/(3) \\ \text{slope = 6} \end{gathered}$

In option D,

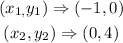
$\begin{gathered} (x_(1,)y_1)\Rightarrow(-1,0) \\ (x_2,y_2)\Rightarrow(0,4\text{)} \end{gathered}$

the slope is thus evaluated as

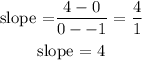
$\begin{gathered} \text{slope =}(4-0)/(0--1)=(4)/(1) \\ \text{slope = 4} \end{gathered}$

Since the slope in option B is evaluated to be -5 which is equivalent to the slope of the function in question, the correct option is B.

Please log in or register to add a comment.