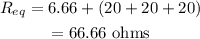Question

Calculate the total resistance for:A. Three resistors, each 20 Ω, connected in series.B. Three resistors, each 20 Ω, connected in parallel.C. Three resistors, each 20 Ω, connected in parallel, which are then connected to three resistors, each 20 Ω, connected in series.

Answer 1

(A)

Given data

*Three resistors, each 20 Ω, connected in series.

Then, the total resistance is calculated as

`\begin{gathered} R_(eq)=R_1+R_2+R_3 \\ =20+20+20 \\ =60\text{ ohms} \end{gathered}`

Hence, the total resistance is R_eq = 60 ohms

(B)

Given data

*Three resistors, each 20 Ω, connected in parallel.

Then, the total resistance is calculated as

`\begin{gathered} (1)/(R_(eq))=(1)/(R_1)+(1)/(R_2)+(1)/(R_3) \\ =(1)/(20)+(1)/(20)+(1)/(20) \\ R_(eq)=6.66\text{ ohms} \end{gathered}`

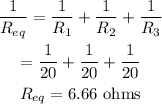
Hence, the equivalent resistance is R_eq = 6.66 ohms

(C)

Given data

*Three resistors, each 20 Ω, connected in parallel, which are then connected to three resistors, each 20 Ω, connected in series.

Firstly, three resistors, 20 ohms are connected in parallel is calculated as

`\begin{gathered} (1)/(R_p)_{}=(1)/(20)+(1)/(20)+(1)/(20) \\ R_p=6.66\text{ ohms} \end{gathered}`

Now, the parallel equivalent resistance is connected with the 20 ohms three series resistors. Then, the total resistors are calculated as

`\begin{gathered} R_(eq)=6.66+(20+20+20) \\ =66.66\text{ ohms} \end{gathered}`