Question

the state lottery board is examining the machine that randomly picks the lottery numbers. on each trial, the machine outputs a ball with one of the digits 0-9, the ball is then replaced in the machine. the lottery board tested the machine for 40 trailsround to the nearest thousandth A) assuming that machine is fair, compute the theoretical probability of getting a 9B) from these results, compute the experimental probability of getting a 9

Answer 1

Question A:

- The theoretical probability is just the ideal probability of choosing a ball labeled 9 from 10 balls.

- This is gotten using the formula below

`P(9)=\frac{\text{ Number of balls labeled 9}}{\text{Total Number of balls}}`

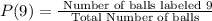
- Thus, we can find the theoretical probability as follows

`P(9)=(1)/(9)\approx0.111\text{ (To the nearest thousandth)}`

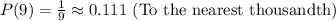
Question B:

- The Experimental probability is the probability based on the experimental values gotten in trials.

- This probability is gotten by the formula below:

`P_E(9)=\frac{\text{Number of trials that resulted in 9}}{\text{Number of trials in total}}`

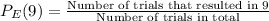
- The experimental probability is given

`P_E(9)=(6)/(40)=0.150\text{ (to the nearest thousandth)}`

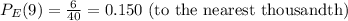
Question C:

- The experimental probability should be equal to the ideal probability for consistency's sake. But many times, we get values not close to the theoretical probability in a few trials.

- But after a large number of trials, the experimental probability becomes more and more like the theoretical probability.

- Thus, the answer to this question is OPTION B

Final Answer

Question A

`P(9)=(1)/(9)\approx0.111\text{ (To the nearest thousandth)}`

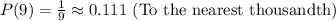
Question B

`P_E(9)=(6)/(40)=0.150\text{ (to the nearest thousandth)}`

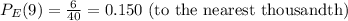
Question C

OPTION B