Given:
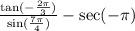
First
Recall
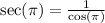
This implies
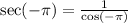
Hence, the given expression becomes
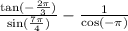
Using calculator
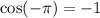
Hence,
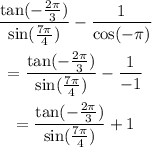
Also,
![\sin ((7\pi)/(4))=-\frac{1}{\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/46smxd6ufla4law8n5kgdjtylh6xlsqggi.png)
This gives
![\begin{gathered} (\tan(-(2\pi)/(3)))/(\sin((7\pi)/(4)))+1 \\ =\frac{\tan(-(2\pi)/(3))}{-\frac{1}{\sqrt[]{2}}}+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mdvafywec1hdlf42myle30xvsduspo8xho.png)
Simplifying the expression gives
![\begin{gathered} \frac{\tan(-(2\pi)/(3))}{-\frac{1}{\sqrt[]{2}}}+1 \\ =\tan (-(2\pi)/(3))/-\frac{1}{\sqrt[]{2}}+1 \\ =\tan (-(2\pi)/(3))*-\sqrt[]{2}+1 \\ =-\sqrt[]{2}\tan (-(2\pi)/(3))+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/soxww0mehmnchk1zzouhfce80yqfk58moa.png)
Using the following property
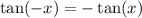
It follows
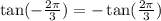
Hence the expression becomes
![\begin{gathered} -\sqrt[]{2}\tan (-(2\pi)/(3))+1 \\ =-\sqrt[]{2}(-\tan ((2\pi)/(3)))+1 \\ =\sqrt[]{2}\tan ((2\pi)/(3))+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/27rhs9lv2i5rlpojgf5050ivddnz87zsd3.png)
And
![\tan ((2\pi)/(3))=-\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/6aefnsfw616zibmkddy300gul21be8g872.png)
This gives
![\begin{gathered} \sqrt[]{2}\tan (-(2\pi)/(3))+1 \\ =\sqrt[]{2}(-\sqrt[]{3)}+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/p7mvkdqkkb4md1n6ohy9s1o5e3y9j8xxkw.png)
Simplifying the expression gives
![\begin{gathered} \sqrt[]{2}(-\sqrt[]{3)}+1 \\ =-\sqrt[]{6}+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bk2hc3rrq8xqr3vj6xdpco09yiqsrgmrz6.png)
Therefore, the answer is
![-\sqrt[]{6}+1](https://img.qammunity.org/2023/formulas/mathematics/college/ajhi3410jtsxtp28mnac1jz0fdgl7kgny2.png)