The Solution:
Given Polly's grades as:
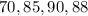
Let the minimum grade she needs to average more than 85 be represented with x.
By formula,
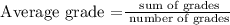
In this case,
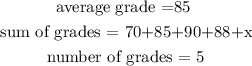
Substituting, we get the inequality that describes the situation as below:

The above inequality is the same as
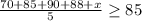
Solving the above inequality, we multiply both sides by 5.
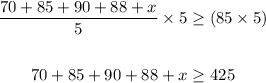
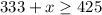
Collecting the like terms, we get
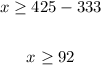
Thus, the minimum grade Polly needs is 92.
Therefore, the correct answer is 92.