Question

Using a given zero to write a polynomial as a product of linear

Answer 1

Given the polynomial:

`g(x)=x^3+9x+20x+6`

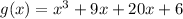
Where:

-3 is a zero of the polynomial.

Let's express the function as a product of linear factors.

Where:

x = -3

Equate to zero:

x + 3 = 0

Using synthetic division, let's divide the polynomial by -3:

Therefore, we have:

`g(x)=(x+3)(x^2+6x+2)`

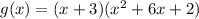
Now,let's solve the expression(quotient) for x using the quadratic formula

`x^2+6x+2`

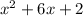
Apply the general quadratic equation:

`\begin{gathered} ax^2+bx+c \\ \\ x^2+6x+2 \end{gathered}`

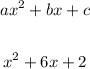
WHere:

a = 1

b = 6

c = 2

Apply the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Hence, we have:

`\begin{gathered} x=\frac{-6\pm\sqrt[]{6^2-4(1)(2)}}{2(1)} \\ \\ x=\frac{-6\pm\sqrt[]{36-8}}{2} \\ \\ x=\frac{-6\pm\sqrt[]{28}}{2} \\ \\ x=(-6)/(2)\pm\frac{\sqrt[]{28}}{2} \\ \\ x=-3\pm\frac{\sqrt[]{4\cdot7}}{2} \\ \\ x=-3\pm\frac{2\sqrt[]{7}}{2} \\ \\ x=-3\pm\sqrt[]{7} \\ \\ x=-3-\sqrt[]{7},-3+\sqrt[]{7} \end{gathered}`

Therefore, the polynomial g(x) as a product of linear factors are:

`g(x)=(x+3)(x+3-\sqrt[]{7})(x+3+\sqrt[]{7})`

ANSWER:

`g(x)=(x+3)(x+3-\sqrt[]{7})(x+3+\sqrt[]{7})`