Question

Hudson travels 1,170 miles in a jet and then 260 miles by car to get to a business meeting. The jet goes 325 mph faster than the rate of the car, and the car ride takes 1 hour longer than the jet. What is the speed, in miles per hour, of the car

Answer 1

Given:

The distance covered by the plane, d_A=1170 miles

The distance covered by the car, d_C=260 miles

To find:

The speed of the car.

Step-by-step explanation:

Let us assume that the speed of the jet and the car is S_A and S_C respectively.

Then from the question,

`S_A=S_C+325\text{ }\to\text{ \lparen i\rparen}`

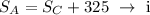
Let us assume the time of ride in the jet and the car is t_A and t_C respectively.

Then from the question,

`t_A=t_C-1\text{ }\to\text{ \lparen ii\rparen}`

The speed of the jet is given by the equation,

`\begin{gathered} S_A=(d_A)/(t_A) \\ \implies d_A=S_At_A\text{ }\to\text{ \lparen iii\rparen} \end{gathered}`

On substituting the equations (i) and (ii) in equation (iii),

`d_A=(S_C+325)(t_C-1)\text{ }\to\text{ \lparen iv\rparen}`

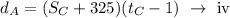
The speed of the car is given by,

`\begin{gathered} S_C=(d_C)/(t_C) \\ \implies t_C=(d_C)/(S_C)\text{ }\to\text{ \lparen v\rparen} \end{gathered}`

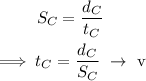
On substituting the equation (v) in equation (iv),

`\begin{gathered} d_A=(S_C+325)((d_(C))/(S_(C))-1) \\ \implies d_AS_C=(S_C+325)(d_C-S_C) \end{gathered}`

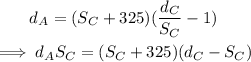
On substituting the known values in the above equation,

`\begin{gathered} 1170S_C=(S_C+325)(260-S_C) \\ \implies1170S_C=-S_C^2-65S_C+84500 \\ \implies S_C^2+1235S_C-84500=0 \end{gathered}`

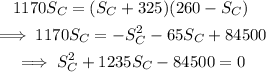
On solving the above equation,

`\begin{gathered} S_C=65\text{ mph or} \\ S_C=-1300\text{ mph} \end{gathered}`

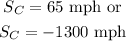
As the car is moving forward, S_C=65 mph

Final answer:

The speed of the car is 65 mph.